3.1 Dealing with twins.
Before getting into the matter: all variables and concepts used till now remain unchanged unless otherwise stated.
In order to avoid confusions though I am going to extract the twin primes from Z, a numerical sequence perfectly comparable to Y, the long zero-string we used to extract the primes from in the previous 2 pages.
So the first thing you should do is to generate Z. In the second place you should decide where to place B, the upper limit of the twins you want to extract. And again, no matter how tempting it is to try to find all the twins that are smaller than some multiple of 10 like one million, or ten millions, or one billion, you should try to find all twins that are smaller than some number that is the square of some element of A. I suggest you take again 2,002,225, the square of 1,415, exactly like we did in the previous pages.
Next you decide is how long Z should be. Well, by now it will not surprise you that this length, n is found with
n = (B -1) / 6
In this case:
n = (2,002,225 -1) / 6 = 333,704
Once Z has been generated and has been given the proper length the checking can begin because yes, finding prime numbers as such and finding the twins both obey to the same principle: you generate a string of zeroes and then you check all places in Z where the twins are NOT. Once your checking is done you find the twins in those positions of Z that have remained unchecked.
As we did in the previous section the checking is done in rounds. All you need to execute a particular round is to find the first element to be checked and the checking frequency.
In Table 4 you find the first 12 rounds you need whenever you start looking for the twins greater than 5 and smaller B.
As for m, the number of checking rounds you need in order to get all twins that are smaller than B,
m = 2(√B \ 3 -1)
where “\” stands for integer division.
In the example given above, if you want to get all twins < 2,002,225:
m = 2(√2002225 \ 3 -1) = 940
At this point it is worth noticing that the first of any pair of twins has always an odd ranking in the original Y (see page 1), implying that the second must be even-ranked. Keeping this in mind, Table 4 was constructed where the single elements stand for the indicated pair of twins in Z. You have to keep in mind though that whereas Y contains single elements of A, Z contains pairs of elements, all grouped at both sides of all multiples of 6.
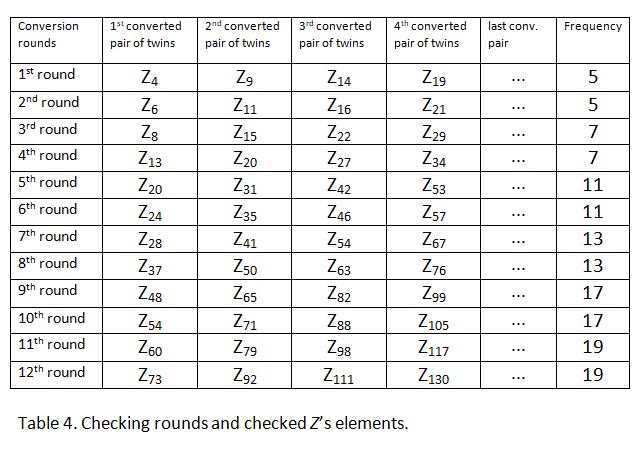
Table 4 can be expanded in exactly the same way as Table 2. The first element of the odd rounds and of the even rounds, as well as the frequencies, have their basis on A. Getting them should offer no difficulty by now.
After checking is completed, the twins are held in Z by proxy by those elements that have conserved their original value of 0. In order to convert all those zero-values into the twins whose place they hold, you simply look at r the ranking of that particular zero in Z and find its corresponding twins p and q as follows:
p = 6r - 1
q = p + 2
which corroborates the very well known fact that twins reside at both sides of multiples of 6.
It is as
simple as that.
2.2 Generating twins indefinitely.
Besides generating the twins from 5 onwards, the present algorithm offers the possibility of generating twins indefinitely, two features that no other algorithm can offer.
As it was said in the previous pages, while extracting the twins from 5 to B, the latter has to be the square of some element of A. Besides, as it was said in the previous section regarding the primes, it holds here also that there are two methods to extract twins indefinitely.
By means of the first method you generate the twins step wise, first from 5 to B, then from B to C and so on.
If you want to use this step wise method to extract your twins, you should perform the following steps:
• While generating twins from 5 to B you save in X the ranking in Z of the very last element of each checking
round.
• The length of X is therefore equal to m, the number of rounds you need in order to extract your twins from 5 to B. If
you set equal B to 2,002,225 as we did before, then the number of checking rounds you need is equal to 940, so your X should
be an array that is capable of containing 940 numbers.
• Once you have performed your first step, you determine the new upper limit of the next series of twins you want to extract,
you generate a new Z, you determine its length and you begin the checking again. You begin your checking at the position
in Z that is indicated by the first element of X and, being it the first checking round, you do your checking
with a frequency of 5. Once your first round is completed, you initiate your second round at the position in Z that is
indicated by the second element of X and being this the second round, you do your checking with a frequency of 5 as well.
• At the end of each round you must not forget to save the last checked position in Z in order to facilitate things for the
next step, the third one.
• But coming back to your second step, once your X is depleted you have to determine the ranking of Z where your
next checking round should begin. With the instructions given on Tables 1 and 4 this should be easily done.
• Once your second step is performed you begin your third step, then your fourth step... until eventually you also run out of
memory. But running out of memory depends on the way you run things on your computer. Table 5 gives an overview of the way the
most important variables grow as B, the upper limit of the twins you want to extract, becomes bigger and bigger. Realising that
n grows very fast gives you the chance to manage your computer’s memory in an adequate manner.
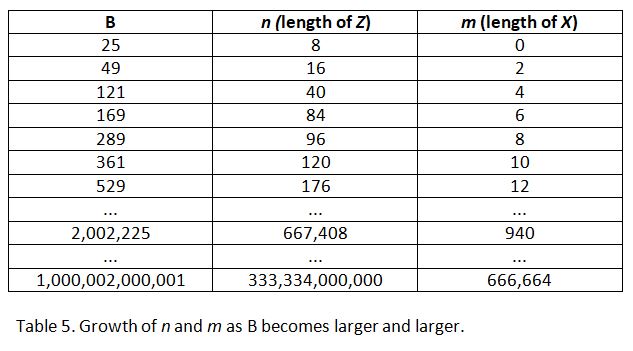
• For people with limited resources the best way to extract as many twins as possible is indeed to go at once from 5 to B, taking B as large as possible and then go ahead and generate all those twins in one single step. If you still have room to go further, begin again from scratch making B larger than the first time. You will eventually run out of memory, anyway.
The second method to deal with the problem is this: instead of extracting twins from 5 to B you can decide to extract
twins that are greater than B instead of smaller than B. This method suits people with more resources and better
programming skills.
This second method consists of computing X instead of constructing it by saving in it the ranking of the
last Z-element that gets checked at the end of each checking round. And you compute X as follows:
• You determine B and B should be the square of an element of A, for instance 2,002,225 that is the square of 1,415.
• You then find the ranking r of B in Z which you find with: r = (B-1)/6. And I repeat: if you want to
apply this method, B has to be the squared value of an element of A.
• Then you initiate your checking rounds on Z. As the frequencies of the checking rounds (see Table 4, last column)
remain unchanged no matter where you decide to initiate your checking on Z, the most important thing now to compute is the
index of the first element of each checking round. You achieve this by first computing c:
c = (r – a) mod b, where:
r is the ranking of B in Z,
a is the index of the very first element of Z to be checked
when you decide to extract all twins that are greater than
or equal to 5 (Table 4, second column),
b is the frequency (Table 4, last column)
• Once you have found c, the ranking in Z where a checking round should begin is determined by:
(B-1)/6 – c
• In order to facilitate things I have computed the first 12 checking rounds needed to find twins that are greater than 2,002,225, see Table 6. Expanding Table 6 is as easy as expanding Table 1.
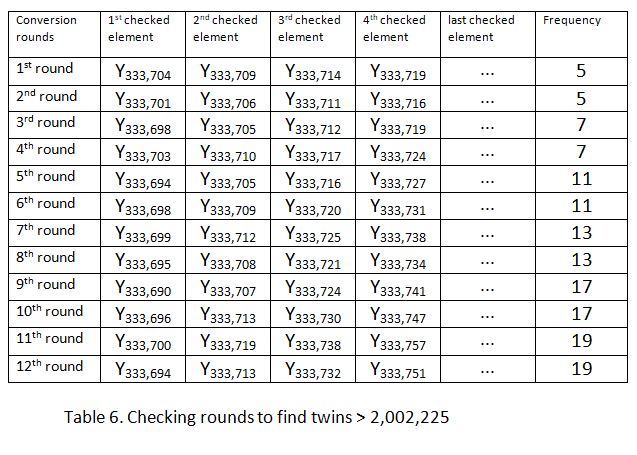
• Expanding Table 6 allows you to look for twins that are greater than 2,002,225. How far you want to go is up to you but remember that B, the new upper limit has to be the square value of an element of A. For instance, letting B being equal to 152,201,569 will do, as it is the square value of 12,337, a number that is divisible neither by 2, nor by 3 and that therefore is an element of A. In such a case you are looking for twins that are greater than 2,002,225 and smaller than 152,201,569.
2.3 Some final remarks on twins.
1. Also Table 4 gets its dynamics from A.
2. Checking rounds should be brought to an end once the algorithm tries to check an element in Z that is greater than B.
3. Once an element of Z has been converted to 1 during a checking round, it never loses that status no matter how often
the same element gets “hit” during subsequent rounds.
4. The dynamics of the algorithm restrict themselves to sieving all pairs of twins of which at least one is not a prime number.
Sieving efficiency is fostered by the absolute absence of divisibility tests. As sieving is done on Z, an ordinally
arranged sequence, the sieving process can be prolonged at wish, without slowing down, no matter how far one decides to go
into ℕ. The process is particularly fast if it is decided to represent Z in memory bit-wise, not byte-wise.
5. Once again, you should keep in mind that in this section twins are referred to as if they were one single unity. To take an
example, the 5th element of Z is the pair [23,25] which by the way is not a twin.
____________________________________________________________________
Click below to order a book.










.
N/A