1.1 Finding the prime numbers.
Finding the prime numbers can mean many things. In this site it means: You take a rather large number, say 10,000,000. You then follow the instructions given in this site. The result will be that you get all prime numbers that are smaller than 10,000,000.
Instead of 10,000,000 you can choose a number that is 10 times larger, or 1000 times larger, or one million times larger i.e. 10,000,000,000,000. You will always get all primes that are smaller than any number you wish.
It is true, if you decide to use the algorithm presented in this site in order to find all prime numbers that are smaller than 10,000,000,000,000, you will have to have some programming skills. But if you have them, all you need is a Ꞓ350-machine (that is what mine is worth anyway) and give it instructions to repeat a certain operation about 1,054,091 times. I am pretty sure that within one hour or so your little machine will come up with all prime numbers that are smaller than 10,000,000,000,000.
In a nutshell what the present algorithm does is this: you generate in your computer a long sequence of zeroes. You then go ahead and check some of those zeroes (this is the exercise you should repeat about 1,054,091 times in the example above). When you are done with the checking there are still many zeroes that have remained unchecked. Well, those are the prime numbers.
So, let us now go ahead and begin. The first thing to do is to decide about how big the largest prime number should be that you intend to generate. Suppose you decide to get all prime numbers that are smaller than about 2,000,000. Look at the word about. The present algorithm will allow you in due course to get exactly all primes smaller than 2,000,000. You will need some training though and the only way to get that is to train yourself by using repeatedly the present algorithm.
What I am now going to do is to explain to you how to get all prime numbers that are smaller than two different quantities: one of them will be a little bit less than 2,000,000 in the example given and the other one will be a little bit more than 2,000,000.
To achieve that you take the next steps:
⦁ Take the square root of the desired quantity. In this case: √2000000 = 1414.21
⦁ For reasons that will become clearer later on, you have a choice between these two squares: 14112 = 1,990,921 and 14152 = 2,002,225 (the 2 mentioned quantities, 1411 and 1415 should be elements of A, see below).
⦁ Then you decide whether you want to extract all primes that are smaller than 1,990,921 or instead those that are smaller than 2,002,225. I propose that you choose 2,002,225. And by the way, I will be calling B this upper limit, irrespective of its size. So B is now equal to 2,002,225.
Once you have decided how large B should be, the upper limit of the primes you intend to extract, you have to generate the sequence of zeroes I was earlier talking about. But before generating it, you have to know how long that sequence should be. First though let us agree that we are going to name that sequence Y, and its length n, where
n = (B -1) / 3
Hence you compute n in the example above as follows:
(2,002,225 – 1) / 3 = 667,408
And that is how long Y should be: Y should contain 667,408 zeroes.
If you have the skills to do it you’d better address your sequence bit wise rather than byte wise. This will reduce the length of the memory you need by a factor of 8 at least. If you don’t know what I am talking about, simply disregard this comment.
Once you generate Y, I propose to call its elements y1 , y2 , y3 ... y667,408.
1.2 Checking.
Once Y is neatly arranged in your computer you begin the checking process. What you are going to check are the elements of Y, the ones I have just called y1 , y2 , y3 ... y667,408.
And then the checking itself. There are many ways to check something. Remember that all 667,408 elements of Y were set equal to zero. Well, I suggest that whenever you check a particular element of Y, you simply convert it to 1.
Then there is a second rule you should keep in mind. Whenever an element of Y has been checked, it never gets unchecked. In other words, once an element of Y has been converted to 1 it never gets its original zero-value back.
Checking is done in rounds. If you look closely at Table 1 you will understand what I mean:
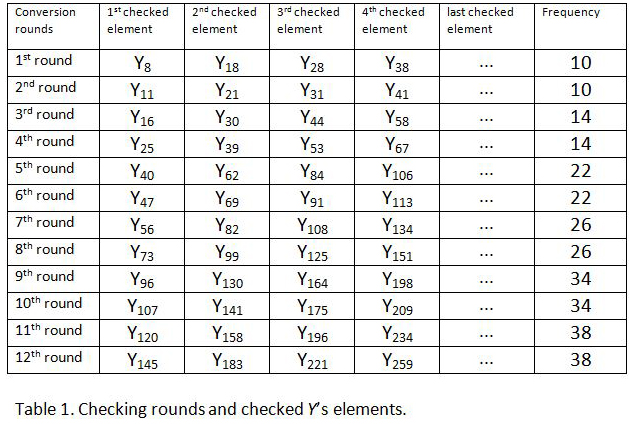
Clarifying the 1st round will make things clear: it means that you look for the 8th element of Y and convert it to 1. Then you look for the 18th element of Y and convert it to 1 as well. Then you convert the 28th element, the 38th element... all the way up until you run out of elements to convert. Arrived at that point you will have concluded your first round.
Then you begin your 2nd round: you convert the 11th element of Y to 1, then the 21st, then the 31st... You now understand what I mean.
If you have chosen a large Y, you will need far more than the 12 checking rounds you see on Table 1. (In the example given above where you were to extract all primes smaller than 2,002,225 you need 940 checking rounds to complete the job, see below). In other words, you need to know how to expand Table 1 to suit your needs. Well, this is very easily done. For that we need to analyse Table 1 a little bit closer.
But before going any further though I will have to clarify a couple of things.
1. In the first place, how to compute m, the number of checking rounds you need, given the upper limit B, of the primes you want to get. You get m as follows:
m = 2(√B \ 3 -1)
where “\” stands for integer division.
In the example given above, if you want to get all primes < 2,002,225:
m = 2(√2002225 \ 3 -1) = 940
2. In the second place, the key to solve the prime numbers problem is a very simple numerical sequence. That sequence has the following 2 properties:
• Its first element is 5,
• It further contains all numbers that are known to you and me, except all multiples of
2 and all multiples of 3.
This is an extremely important sequence and I am going to name it sequence A. Applying the rules just mentioned, A will contain the following elements:
A = 5, 7, 11, 13, 17, 19, 23, 25, 29, 31, 35, 37, 41, 43, 47, 49...
And now that you know A, you are ready to expand Table 1. If you take a close look at the first element of the odd rounds on Table 1, you will see that they are closely related to A:
1st round: (52 -1)/3 = 8
3rd round: (72 -1)/3 = 16
5th round: (112 -1)/3 = 40
7th round: (132 -1)/3 = 56
9th round: (172 -1)/3 = 96
11th round: (192 -1)/3 = 120
And after that, look at the first element of the even rounds:
2nd round: 5x2 + 1 = 11
4th round: 7x2 + 11 = 25
6th round: 11x2 + 25 = 47
8th round: 13x2 + 47 = 73
10th round: 17x2 + 73 = 107
12th round: 19x2 + 107 = 145
After seeing how easy it is to generate the very first element of each checking round, you only have to look at the last column of Table 1 to know where the frequencies come from:
1st and 2nd rounds: 5x2 = 10
3rd and 4th rounds: 7x2 = 14
5th and 6th rounds: 11x2 = 22
7th and 8th rounds: 13x2 = 26
9th and 10th rounds: 17x2 = 34
11thand 12th rounds: 19x2 = 38
As you can easily see, Table 1 can be expanded indefinitely. All you have to do is to instruct your computer to generate the first element of a round and the frequency with which the checking process has to be executed. The machine will then go ahead and execute conversion after conversion, round after round, after round... you only have to take care that the machine does not attempt to start a new round at a position beyond the last element of Y.
After all the checking is done, if you take a look at your Y, you will see that it now contains zeroes and ones, far more ones than zeroes, though. Well, the zeroes that Y now contains are the prime numbers that you were looking for when you began the whole exercise. Although, not exactly. After all, zero is not a number, let alone a prime number.
You have to look at all those zeroes in Y as being the place holders of the real prime numbers. Any two zeroes in Y, although identical, differ only in one aspect: they occupy a different place (ranking) in Y. Well, it is their ranking in Y that makes them suitable to extract from them the prime numbers whose place they hold in Y. If we agree to call r the ranking of any zero in Y, then you extract its corresponding prime number p from Y by stating:
p = 3r + 2 if r is odd, or
p = 3r + 1 if r is even.
Two examples will clarify this completely. You probably remember that if we want to extract all prime numbers that are smaller than 2,002,225, we have to generate Y with a length of 667,408 zeroes. Once all 940 checking rounds have been completed, if you select the zero that occupies the 1,067th position (odd) in Y and also the zero that occupies the 646,002nd position (even) in Y, this is how you convert them to their corresponding primes:
3 x 1,067 + 2 = 3,203, which is a prime number.
3 x 646,002 + 1 = 1,938,007, which is a prime number.
So, generally speaking, given a particular Y, we can say that any prime number p < B can be reduced to the following simplistic expression:
p = 3r + a
where:
• r is the ranking of a 0-element in Y after Y has been checked,
• a = 2 if r is odd, else a = 1.
It is as easy as that.
____________________________________________________________________
Click below to order a book.








.
N/A