2.1 Generating primes indefinitely
While generating rather large amounts of primes, computers tend to run out of memory. The present algorithm is no exception to that. But besides facilitating the extraction of far more primes than any other algorithm, the present one will perform the job much faster.
Before entering into the matter though, a word of caution while choosing the upper limit B of the primes you want to extract. We all have the tendency to choose multiples of 10. We all want to see all primes that are smaller than 100,000 or than 1,000,000, or than one hundred billion. I have said it before: in due course you will be able to do it but for now you’d better restrict yourself to take the square of any element of A as the upper limit B, of your primes (remember: A contains only numbers that are greater than or equal to 5 and that are not multiples of 2 or of 3).
The first method to deal with this problem is this: you generate the primes step wise, first from 5 to B, then from B to C and so on (remember: 5 is the smallest element of A). As you know by now, generating primes with the present algorithm is no other thing than checking Y. Once Y has been checked in the proper manner, the extraction of the primes is an utterly easy exercise.
If you want to use this step wise method to extract your primes, you should perform the following
steps:
• While generating primes from 5 to B you save in X the ranking in Y of the
very last element of each checking round.
• The length of X is therefore equal to m, the number of rounds you need
in order to extract your primes from 5 to B. Remember though that B is the upper limit of
the primes you are looking for during your first step and that therefore B should be the
square of some element of A. Going back to an example I have given before, suppose
you have chosen B to be 2,002,225, in other words that during your first step you want to
extract all prime numbers that are smaller than 2,002,225. We have seen that the number of
checking rounds you need is equal to 940, so your X should be an array that is capable
of containing 940 numbers.
• Once you have performed your first step, extracting your primes and saving them somewhere,
you determine the new upper limit of the next series of primes you want to extract, you generate
a new Y, you determine its length and you begin the checking again. You begin your
checking at the position in Y that is indicated by the first element of X and,
being it the first checking round, you do your checking with a frequency of 10. Once your
first round is completed, you initiate your second round at the position in Y that is
indicated by the second element of X and being this the second round, you do your
checking with a frequency of 10 as well. A word of caution: you have to arrange things in your
computer in such a way that your new Y is a prolongation of the Y you used
during your first step.
• At the end of each round you must not forget to save the last checked position in Y
in order to facilitate things for the next step, the third one.
• But coming back to your second step, once your X is depleted you have to determine
the ranking of Y where your next checking round should begin. With the instructions
given in the preceding page this should be easily done.
• Once your second step is performed you begin your third step, then your fourth step...
until eventually you also run out of memory. But running out of memory depends on the way you
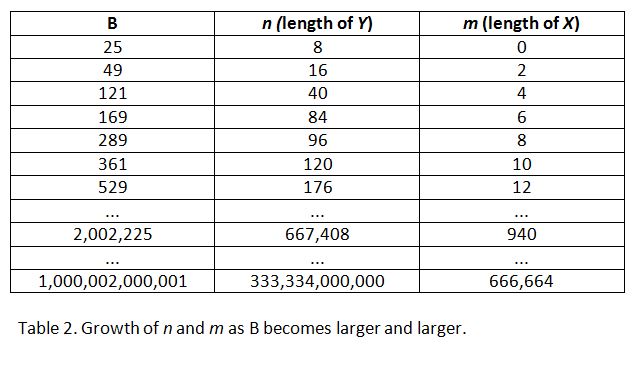
run things on your computer. Table 2 gives an overview of the way the most important variables
grow as B, the upper limit of the primes you want to extract, becomes bigger and bigger.
Realising that n grows very fast gives you the chance to manage your computer’s memory
in an adequate manner.
• For people with limited resources the best way to extract as many primes as possible is
indeed to go at once from 5 to B, taking B as large as possible and then go ahead and generate
all those primes in one single step. If you still have room to go further, begin again from
scratch making B larger than the first time. You will eventually run out of memory, anyway.
The second method to deal with the problem is this: instead of extracting prime numbers
from 5 to B (the present algorithm gives no room to extract 2 and 3 as primes, so they are not
considered to be primes) you can decide to extract prime numbers that are greater than
B instead of smaller than B. This method suits people with more resources and better
programming skills than people like me.
This second method consists of computing X instead of constructing it by saving in it
the ranking of the last Y-element that gets checked at the end of each checking round.
And you compute X as follows:
• You determine B and B should be the square of an element of A, for instance 2,002,225
that is the square of 1,415.
• You then find the ranking r of B in Y which you find with: r = (B-1)/3.
And I repeat: if you want to apply this method, B has to be the squared value of an element of
A.
• Then you initiate your checking rounds on Y. As the frequencies of those checking
rounds (see Table 1, last column) remain unchanged no matter where you decide to initiate your
checking on Y, the most important thing now to compute is the index of the first element
of each checking round. You achieve this by first computing c:
c = (r – a) mod b, where:
r is the ranking of B in Y,
a is the index of the very first element of Y to be checked
when you decide to extract all primes that are greater than
or equal to 5 (Table 1, second column),
b is the frequency (Table 1, last column)
• Once you have found c, the ranking in Y where a checking round should begin is determined by:
(B-1)/3 – c
• In order to facilitate things I have computed the first 12 checking rounds needed to find primes that are greater than 2,002,225, see Table 3. Expanding Table 3 is as easy as expanding Table 1.
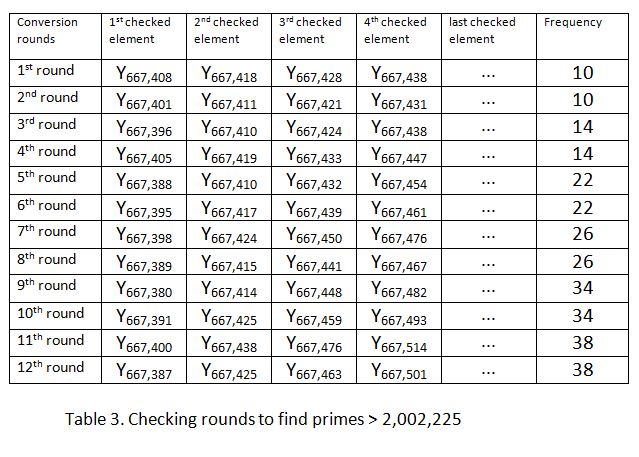
• Expanding Table 3 allows you to look for primes that are greater than 2,002,225. How far you want to go is up to you but remember that B, the new upper limit has to be the square value of an element of A. For instance, letting B being equal to 152,201,569 will do as it is the square value of 12,337, a number that is divisible neither by 2, nor by 3 and that therefore is an element of A. In such a case you are looking for primes that are greater than 2,002,225 and smaller than 152,201,569.
• Once you complete your checking rounds you extract your primes from Y in exactly the same way that was explained before.
2.2 Counting primes.
Oftentimes people want to know the amount of primes that are smaller than a certain number, mostly a multiple of 10. There are three ways to achieve this (beware though that the present algorithm does NOT consider 2 and 3 to be primes):
• The first one is to generate all primes that are smaller than say two billion and then count them.
• The second way is much easier: you generate Y, you check it and once you finish your checking you simply count the number of zeroes that you find in Y: that is exactly the amount of primes that you are looking for.
• There is a third way, but this one is of statistical nature. It will only approximate
the result you are looking for and it is far more time consuming. It is presented here only for
the sake of completeness.
Beware that in the remainder of this section I am going to talk about checking A, not Y, as I should. On the other hand Y is no other thing than a placeholder of A. Beginning with checking rounds 1 and 2, and knowing that they check 2 out of every 10 elements of A, your best guess is that these rounds will check 1 fifth of all elements between the 8th element of A and B, the upper limit of the primes you are looking for.
Checking rounds 3 and 4 taken together check 1 out of every 7 A-elements. So, from the starting point of round 3 (and 4) you have 4 rounds running: 2 of them checking conjunctively every 5th element and the other 2 checking also conjunctively every 7th element. So, theoretically they add up checking (1/5 + 1/7) = 0.3429 % of the remaining elements of A.
But from the starting point of round 3 onwards there is a chance that rounds 3 and/or 4 will
check an element that has already been checked by rounds 1 or 2, so you will have to correct
for that. Once this correction is applied it appears that the probability of an A-element
being checked between the starting point of round 3 and B, the upper limit of the primes you are looking
for, has to be brought back to 0.3143 %. This implies that as far as the first 4 checking rounds
are concerned, the A-elements situated between the initial point of round 3 and B have a
probability of 0.6857 % of remaining UNchecked, i.e. of being primes.
Checking rounds 5 and 6 check together 1 out of every 11 elements, you do your home work
computing the probability of an element being checked that is situated after the initial
point of round 5, you apply your correction, and so forth.
So, this is how you compute your probabilities. The starting point of every odd checking round reduces the probability of the remaining elements of A being primes whereas the subsequent correction enhances it. In the long run they sort of keep one another in balance, reducing very, very slowly the probability of an A-element being a prime without ever reducing that probability to zero.
There are many ways to try to deduce statistically the number of primes that are smaller than certain quantities. Should you work this procedure out, then your results should be comparable to the ones below, that I took from the Internet:
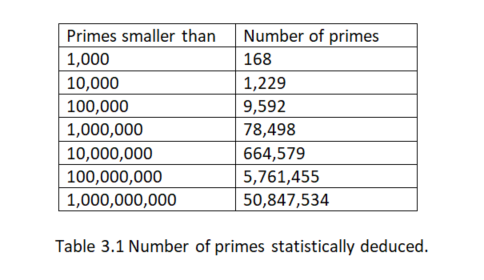
As you see, this is a quite cumbersome procedure and I wouldn’t bother using it other than to compare its results with some of the mathematicians’ famous “conjectures”, the ones they very much love to prove true or false. But, should you decide anyway to apply this procedure to count your primes, you should not forget to add 7 to your final results, being the first 7 primes, from 5 to 23, that were left out of the statistical procedure.
2.3 Some final remarks on primes.
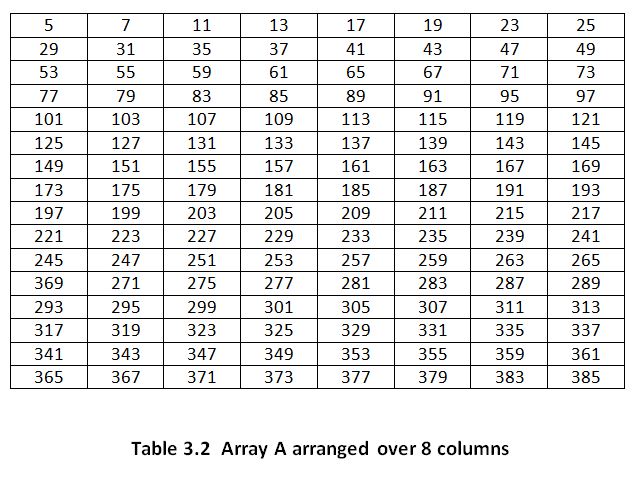
1. In the preceding sections array A (“the mother of all primes”) has been quoted repeatedly. If you are inclined to learn by intuition I suggest you take a good look at table 3.2. Notice particularly the increment of 24 that takes place column-wise over all columns.
2. In the second place it is extremely useful to look at the elements of Y that get checked as a result of the checking rounds taken two by two. So on the first row of Table 3.3 you see the places of Y that get checked during the first and second rounds, on the second row the checking of Y during the third and fourth rounds...
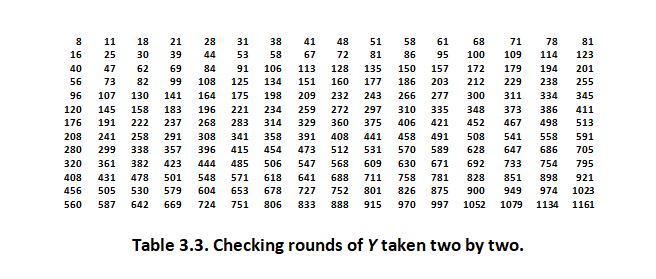
3. And finally, on Table 3.4 you can take a look at the actual elements of A that get checked as a result of the preceding table:
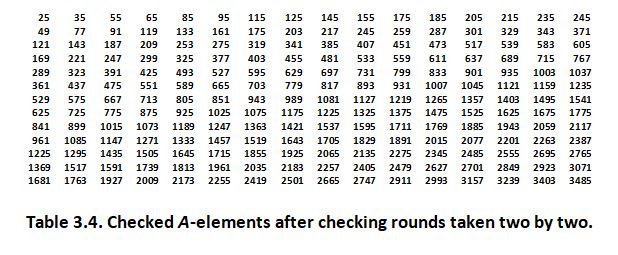
If you care to expand these 3 tables in Excel and again, if you are inclined to learn by intuition, you will be surprised to see how much you can learn from them.
____________________________________________________________________
Click below to order a book.











.
N/A